Optimal Transport 02. エントロピー正則化
01. はじめ
02. エントロピー正則化
03. Unbalanced Optimal Transport
Cuturi1 の論文をもとに、Optimal Transportのエントロピー正則化について考えていきましょう 。
計算量#
$r$ から $c$ へのOptimal Transportは次のようになります
$$
\large
d_\mathbf{M}(r, c) \triangleq \min_{\mathbf{P}\in\mathbf{U}(r, c)} \langle \mathbf{P}, \mathbf{M} \rangle
$$
ここで、$\mathbf{M} \in \mathbb{R}^{d\times d}$ はcost matrixです
計算量について考えると、どのような行列$\mathbf{M}$に対しても最悪のケースで $O(d^3 \log d)$となります。
エントロピー正則化#
ここで、Optimal Transportにエントロピー正則化を導入します。
まず、同時確率分布に対する次の不等式が成り立ちます
$$
\forall r, c \in \Sigma_d, \forall \mathbf{P} \in \mathbf{U} (r, c), h(\mathbf{P}) \leq h(r) + h(c)
$$
また、$h(rc^\mathsf{T}) = h(r) + h(c)$ より次式が成り立ちます
$$
\begin{eqnarray*}
\mathbf{U}_\alpha (r, c) &\triangleq& \lbrace \mathbf{P} \in \mathbf{U} (r, c) \mid \mathrm{\bf KL}(\mathbf{P} \Vert rc^\mathsf{T}) \leq \alpha) \rbrace \\\
&=& \lbrace \mathbf{P} \in \mathbf{U} (r, c) \mid \mid h(\mathbf{P}) \geq h(r) + h(c) - \alpha \rbrace \\\
&\subset& \mathbf{U}(r, c)
\end{eqnarray*}
$$
ここで、$\mathrm{\bf KL}(\mathbf{P} \Vert rc^\mathsf{T}) = h(r) + h(c) - h(\mathbf{P})$
このように定義した同時分布に対して、Optimal Transportを解きます (得られた値を “Sinkhorn Distance” と呼びます) 。 $$ \large d_{\mathbf{M}, \alpha} (r, c) \triangleq \min_{\mathbf{P}\in \mathbf{U}_{\alpha}(r, c)}\langle \mathbf{P}, \mathbf{M} \rangle $$
このようにエントロピーを考える理由は2つ
- 計算量的な問題
- 解をより"スムーズ"にしたい
1については後で説明するとして、まず2について説明します。前回 説明したように、 輸送計画行列 $\mathbf{P}$ は次の制約条件に従います $$ \mathbf{P}\mathbf{1}_d = r \mathrm{\quad and\quad } \mathbf{P}^\mathsf{T}\mathbf{1}_d = c $$ つまり、制約の個数は $2d$ 個となり、$\mathbf{P}$ は $0$ でない要素が $2d-1$ 個だけあって、それ以外は $0$ であるようなスパースな行列で制約を満たせるということです。 そこで、これを防ぐ (=行列をスムーズにする) ためにエントロピー正則化が必要となってくる。というわけです
Sinkhorn’s Algorithm#
エントロピーで制限されたSinkhorn Distanceを考えます
$$
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
d_\mathbf{M}^\lambda(r,c) \triangleq \langle \mathbf{P}^\lambda, \mathbf{M} \rangle\ \\\
\mathrm{where}\ \lambda > 0 ,\ \mathbf{P}^\lambda = \argmin_{\mathbf{P}\in \mathbf{U}(r, c)} \langle \mathbf{P}, \mathbf{M} \rangle - \frac{1}{\lambda} h(\mathbf{P})
$$
ここで、それぞれの $\alpha$ はある $\lambda\in [0, \infty]$に対応します。
$$
d_{\mathbf{M}, \alpha} (r, c) = d_\mathbf{M}^\lambda (r, c)
$$
そして、この $d_\mathbf{M}^\lambda$ はもとの問題 ($=d_\mathbf{M}$) よりもはるかに低コストで計算できるのです。
Computing $d_\mathbf{M}^\lambda$#
$\lambda > 0$ に対して、$\mathbf{P}^\lambda$ はuniqueで、また、次の形式で表されます2
$$
\mathbf{P}^\lambda = \mathrm{diag}{(u)} \mathbf{K} \mathrm{diag}(v) \\\
\mathrm{where}\ u, v \in \mathbb{R}^d \mathrm{\ and\ non–negative}\\\
\mathbf{K} \triangleq \exp(-\lambda \mathbf{M})\quad \mathrm{(element–wise\ calculation)}
$$
そして、このとき$u, v$は解にiterativeに近づけていくことができます $$ (u, v) \leftarrow (r_\cdot/\mathbf{K}v, c_\cdot/\mathbf{K}‘u) $$
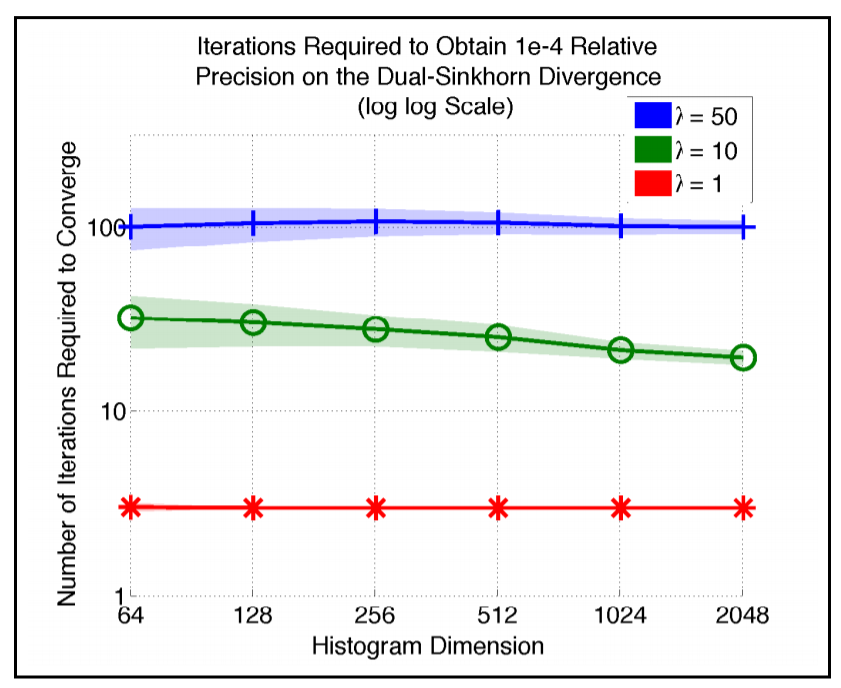
Empirical Complexity#
histgramの次元数に対する収束までに必要なiteration数は下図 (画像は元論文1 引用)