Optimal Transport 03. Unbalanced Optimal Transport
01. はじめ
02. エントロピー正則化
03. Unbalanced Optimal Transport
Optimal Transportの拡張系であるUnbalanced Optimal Transportについて紹介します．
Unbalanced Optimal Transport (Unbalanced OT)#
まず，式を見ていきましょう． $$ L_\mathbf{C}^\tau (\mathbf{a}, \mathbf{b}) = \min_{\mathbf{P}\in\mathbb{R}_+^{n\times m}} \langle \mathbf{C}, \mathbf{P} \rangle +\tau_1\mathbf{D}_\varphi(\mathbf{P}\mathbb{1}_m|\mathbf{a}) + \tau_2\mathbf{D}_\varphi(\mathbf{P}^\mathsf{T}\mathbb{1}_n|\mathbf{b}) $$ 第1項は通常のoptimal transportでの最小化目標です．そして，この第2, 3項が追加されたものとなります．$\mathbf{D}_\varphi(\cdot|\cdot)$ はズレを表す関数で，例えば，euclideanだったりKL距離だったりが考えられます．そして，$\tau_1, \tau_2$はそれらのズレに対するペナルティの大きさを表しています．つまり，$\tau_1 = \tau_2 \rightarrow +\infty$のときズレを許さない，つまり，“balanced"な (通常の) optimal transportとなります．また，$\mathbf{D}_\varphi = \mathbf{KL}$ で，$\tau_1 = \tau_2 \rightarrow 0$ のとき，Hellinger距離と呼ばれる距離となります． $$ \mathrm{L}(\mathbf{a}, \mathbf{b}) = \sum_i(\sqrt{\mathbf{a}_i} - \sqrt{\mathbf{b}_i})^2 $$
Unbalanced OTの計算にもSinkhorn’s iterationを使うことができます．updateは次の式を順番に行うことで行われます，
$$
\mathbf{u} \leftarrow \Bigl( \frac{\mathbf{a}}{\mathbf{Kv}}\Bigr)^{\tau_1/(\tau_1 + \varepsilon)} \quad \mathrm{and} \quad \mathbf{v} \leftarrow \Bigl(\frac{\mathbf{b}}{\mathbf{K}^\mathsf{T}\mathbf{v}}\Bigr)^{\tau_2/(\tau_2 + \varepsilon)}
$$
Unbalanced OTのイメージは次のようになります．
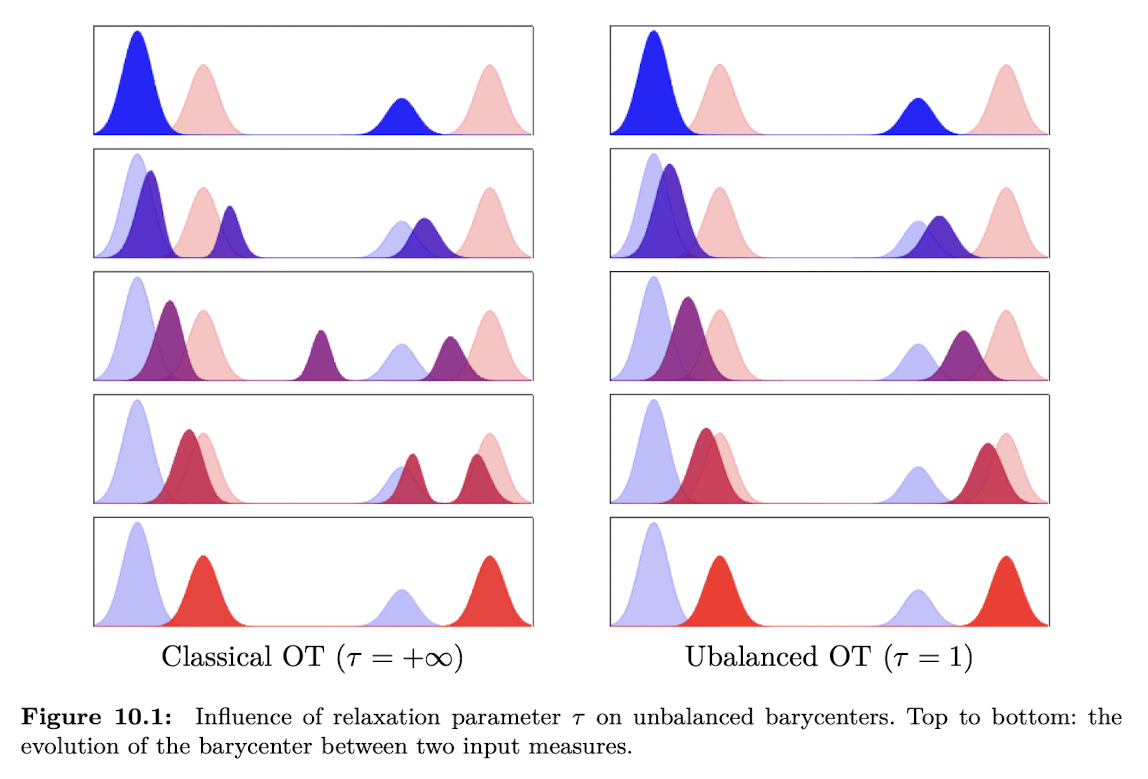
左図がClassical OT (通常のoptimal trasnport) 右図がUnbalanced OTを表しています． Classical OTのとき．左側の山が２つに分散し，右側の山と合流して輸送が行われています． それに対して，Unbalanced OTでは左側の山は左側に，右側の山は右側に移動しています． つまり，Unnbalanced OTは，より"柔軟な"輸送がなされているといえます．
実際の応用としては，input dataがノイジーだったり完全に分かっていないときに，classical OTよりunbalanced OTのほうが優れていることが多いようです．