FNet: Mixing Tokens with Fourier Transforms を読む

FNet: Mixing Tokens with Fourier Transforms
[Thorp et al. arXiv 2020] という論文を読んでいきます. (本文中の図は論文より引用).

Contributions:

  1. token “mixing” 変換がテキストデータにおける多様なsemanticsを十分に捉えられることを示した
  2. self-attention層をFourier Transform層に置き換えたTransformer-likeな FNet というモデルの提案
  3. 学習速度が早く (TPUでは短いシークエンスのときのみ), 精度も良い. また, メモリ使用量も比較的少なくすむ

Model#

Background: discrete Fourier Transforms#

シークエンス $\lbrace x_n \rbrace$ $\left( n \in [0, N-1] \right)$ が与えられたとき, discrete Fourier Transform (DFT) は次のように表される.

\begin{align*} X_k &= \sum_{n=0}^{N-1} x_n \exp\left(-\frac{2\pi i}{N}nk\right), & 0\leq k \leq N-1 \end{align*}

DFTを計算する方法は主に2つ

  1. FFT
    Cooley-Tukeyアルゴリズム
  2. DFT matrixを入力シークエンスに掛ける
    Vandermonde matrix
    TPUでの, 相対的に短いシークエンスに対するDFTだとFFTより早い (基本的にはFFTのほうが早いみたいです) .

FNet architecture#

アーキテクチャを下図に示す. FNetは Fourier mixingレイヤーのあとにfeed-forwardレイヤーが続く構成となっている.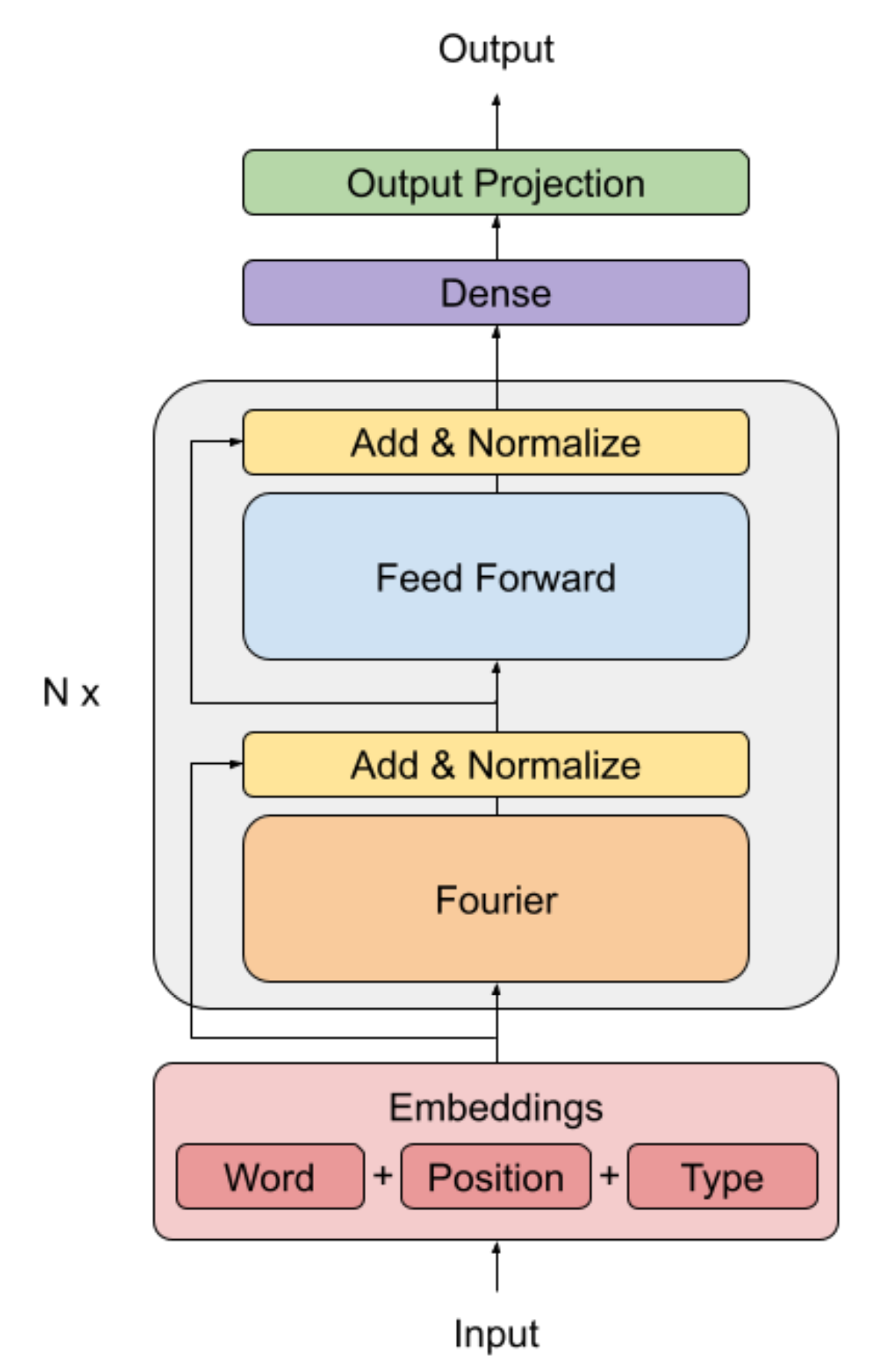

FNet encoder architecture
Figure . FNet encoder architecture

Transformerのencoderのself-attention層をFourier層に置き換えたもので, Fourier層では 2D Fourier変換を用いる. (シークエンス長, 隠れ層の次元数)

つまり, 1D Fourier変換を隠れ層に対して行い, その後, 1D Fourier変換をシークエンスに対して行う. \begin{align*} y = \mathfrak{R}(\mathcal{F}_\mathrm{seq} (\mathcal{F}_{\mathrm{hidden}}(x))) \end{align*} ここで, Fourier変換の結果のうち実部だけ考慮する (虚部は無視する)

Fourier Transformを利用する意味としては, token を合成するのに有効なメカニズムであることがあげられる. Fourier変換は双対性があるため, 実空間と周波数空間を交互に行き来できる. そして, 実空間での畳み込み演算が, 周波数空間での掛け算になるため, FNetは畳み込みを代替できていると考えられる.

Results#

Transfer Learning#

以下のモデルについて検討した

  • BERT-Base
  • FNet encoder
    self-attention層をFourier層に置き換える
  • Linear encoder
    self-attention層を2つの学習可能な線形 (dense) 層に置き換える
  • Random encoder
    self-attention層を2つの定数行列に置き換える
  • Feed forward-only (FF-only)
    Transformerからself-attention層を除いたもの (feed forward層のみ残る)

Masked language modelling pre-training

結果を下表に示す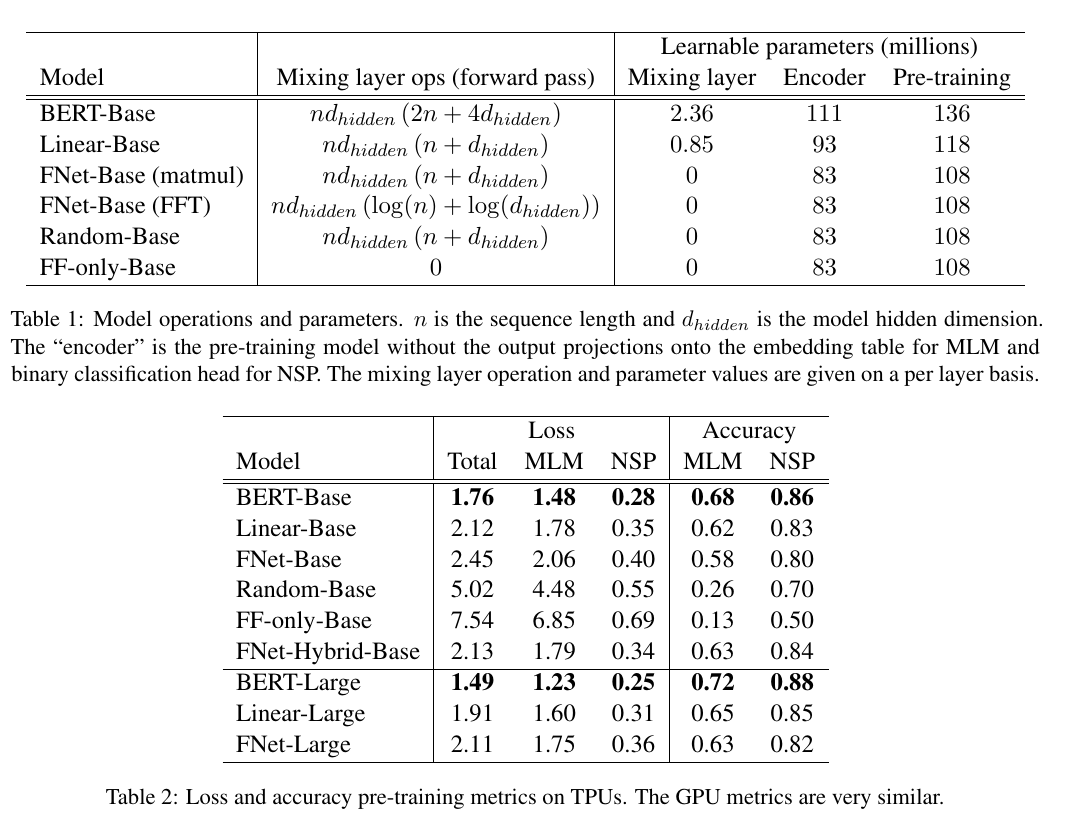

Prepared Models and Results
Figure 1. Prepared Models and Results
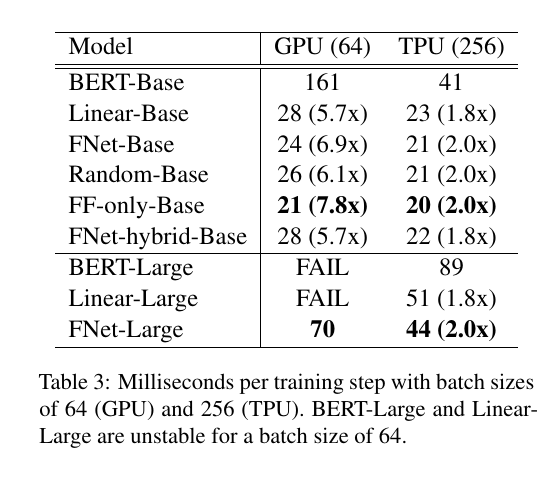
Milliseconds per training step
Figure 2. Milliseconds per training step

FNetとLinear modelは結果こそBERTに劣るものの, スピードはかなり早く, よいトレードオフを達成している. ここで, FNetで使われる2D-Fourier Transformは2つの複素行列の掛け算で表されるため, Linear modelはFourier Transformを再現することはできないが, Linear encoder modelは十分flexibleに予測できるということが推測される. そして, FNetはLinear modelよりパラメータが少なく, 学習速度が早い.

BERTの性能が良いのは, 他のモデルよりも多くのパラメータを持っているから.といったわけではない (BERT-Base のほうがその2倍のパラメータ数を持つFNet-Largeより性能が良い）. これは, BERTのattention weightsがタスクに特化していて, かつ, token dependentであるためと考えられる.

最後の2つのFourier層をself-attention層に置き換えたhybrid FNet modelを作成したところ, 小さなコストで大きな精度向上を達成した.

その他結果は元論文で

References#

© 2024

FNet: Mixing Tokens with Fourier Transforms を読む