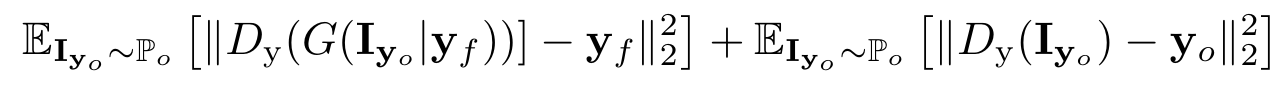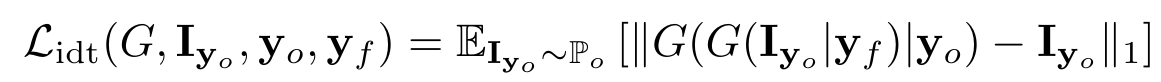GANimation を読む
$$ \def\image#1{\mathbf{I}_{\mathbf{y}{\scriptsize{#1}}}} $$
GANimation: Anatomically-aware Facial Animation from a Single Image
[Pumarola et al. ECCV 2018] という論文を読んでいきます. (本文中の図は論文より引用).
Action Units (AU) アノテーションに基づいたGAN
$\image{r}$ (緑色で囲われた画像) は入力画像. そして, $\alpha$ はsmiling-like expressionに関するAUをコントロールするパラメータ
Introduction#
motivation: single imageからfacial expressionを操作する $\rightarrow$ 映画業界, 写真技術, ファッションやe-コマースに役立つ
facial expression は, discreteでも少ないクラスでも表されない表情筋によって作られるものである. Facial Action Coding System (FACS) [Ekman et al.] は 解剖学的に特定の表情筋の収縮に関わるAction Units (AUs) を表すために提案されたものである. AUの数は少ないが, $7000$もの異なる組み合わせがあることがわかっている.
同じ人の異なる表情が必要になるのを避けるために, 問題を2つに分ける
- AU-conditioned bidirectional adversarial architecture
1つの訓練画像が与えられた時, まず, 欲しい表情の新しい画像を作る. そして, この作られた画像を生成画像のphotorealismに対するロスを取り入れる. - 画像の中で, 新しい表情の伝達に関わる部分に対してフォーカスするattention layerを用いることでSOTAを達成.
Problems Formulation#
任意のfacial expressionのRGB画像は次のように表される: $\image{r} \in \mathbb{R}^{H\times W \times 3}$
また, すべてのgesture expressionは $N$ 個のAUにエンコードされる $\mathbf{y}_r = (y_1, \ldots, y_N)^\mathsf{T}$
(それぞれの要素は$0–1$に正規化される). 連続的なラベルなので, 異なる表情間の自然なinterpolationが可能となる.
目的は, 画像間のマッピングを行う $\mathcal{M}$ を学習すること. \begin{align*} \mathcal{M}: (\image{r}, \mathbf{y}_g) \rightarrow \image{g} \quad (\text{conditioned on AU target }\mathbf{y}_g) \end{align*} つまり, $\image{r}$ を AU label $\mathbf{y}_g$ をもつ画像に変換する.
この学習は $M$個のtriplets: \begin{align*} \lbrace \image{r}^m, \mathbf{y}_r^m, \mathbf{y}_g^m \rbrace \quad (m=1, \ldots, M) \end{align*} を用いてunsupervisedに行われる. ここで, $\mathbf{y}_g^m$ はランダムに生成されたtarget vector. そして, この手法では, 同じ人の異なる表情や expected target image $\image{g}$ を必要としない.
Approach#
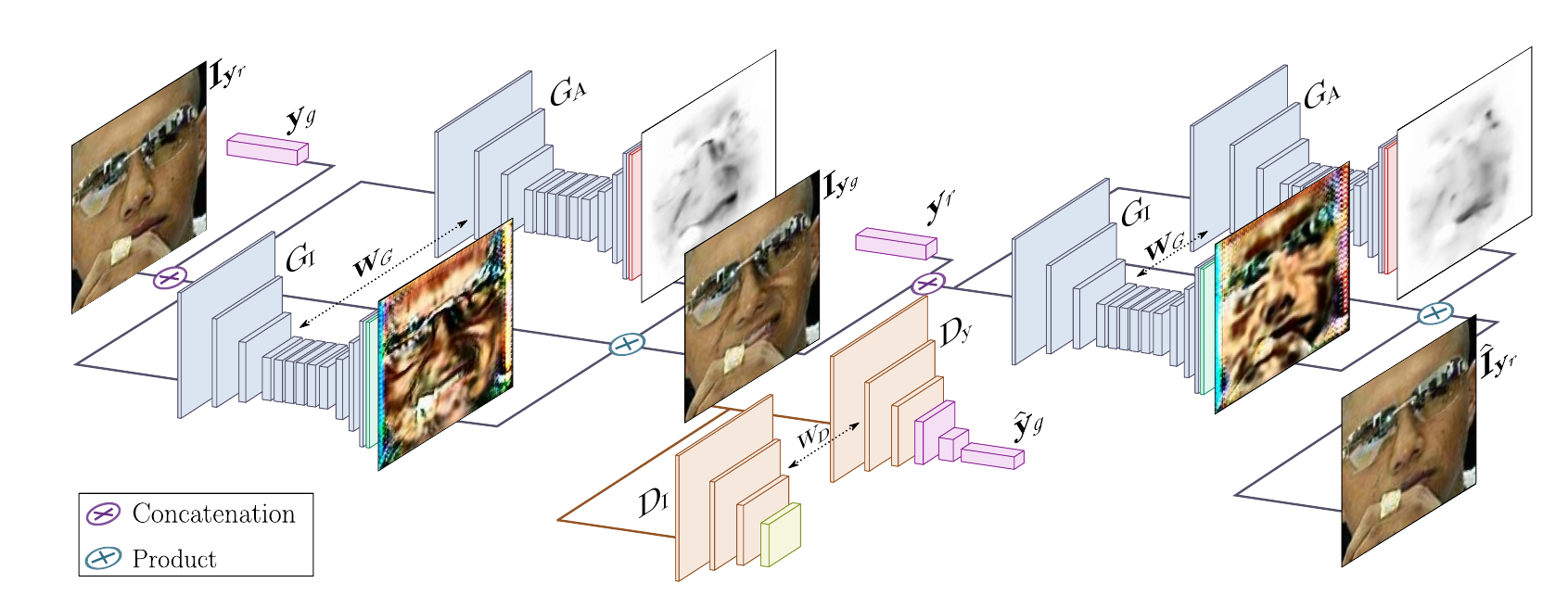
Generator: $G(\image{r} | \mathbf{y}_g)$
このgeneratorは2回使われる
- $\image{r} \rightarrow \image{g}$ (map the input image)
- $\image{g} \rightarrow \hat{\mathbf{I}}_{\mathbf{y}{\scriptsize{r}}}$ (render back)
Discriminator: $D(\image{g})$
WGAN-GPを用いた, 生成画像のqualityと表情を評価するもの
Network Architecture#
Generator
画像 $\image{o} \in \mathbb{R}^{H\times W \times 3}$ と $N$次元ベクトルにエンコードされた感情 (desired expression) $\mathbf{y}_f$ が与えられたとき, generatorに対する入力は次のようになる $$ (\image{o}, \mathbf{y}_o) \in \mathbb{R}^{H\times W \times (N+3)} $$ ($\mathbf{y}_o$は$\mathbf{y}_f$のブロードキャストしたもの Code )
下図にgeneratorのアーキテクチャを示す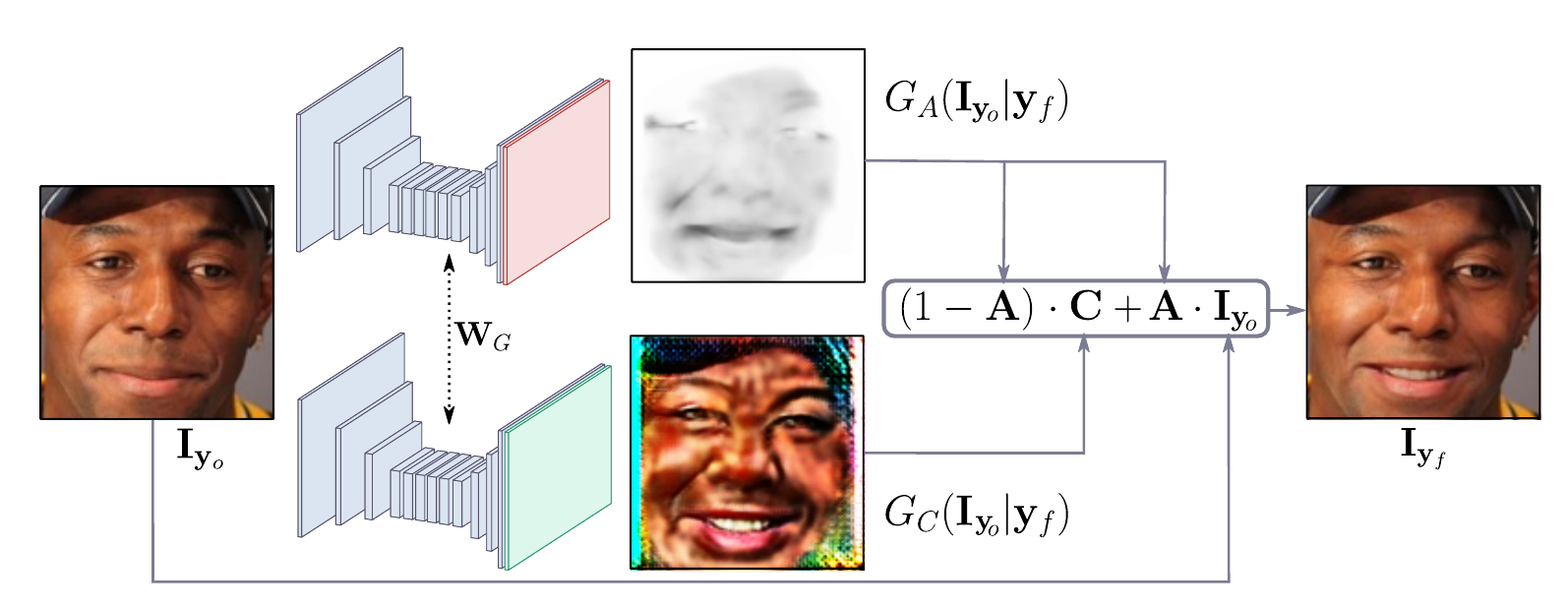
$\mathbf{A}$ は $\mathbf{C}$ が生成した画像のそれぞれのピクセルに対する重要性を表す.
Conditional Critic
$D$ のアーキテクチャはPatchGAN
に似たものである.
PatchGANでは, 入力画像を $\mathbf{I}$ とすると, $\mathbf{Y}_\mathbf{I} \in \mathbb{R}^{H/2^6 \times W / 2^6}$を生成する.
ここで, $\mathbf{Y}_\mathbf{I} [i, j]$ は patch $ij$ が (生成されたフェイク画像ではなく) 真の画像であるかを表す確率である. その最終層にregression headを追加し, 画像のAUs activation $\hat{\mathbf{y}} = (\hat{y}_1, \ldots, \hat{y}_N)^\mathsf{T}$ を推測する
Learning the Model#
ロス関数は4つの項からなる. (細かな定義などは論文参照)
1. Image Adversarial Loss $\mathcal{L}_\mathbf{I}$
Earth Mover Distanceを用いたWGANを参考にする.
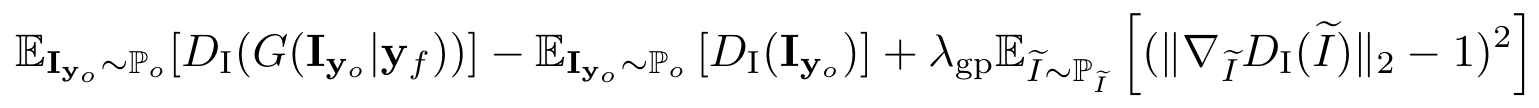
2. Attention Loss $\mathcal{L}_\mathbf{A}$
attention maskが1になる (サチる) ことを防ぐためのロス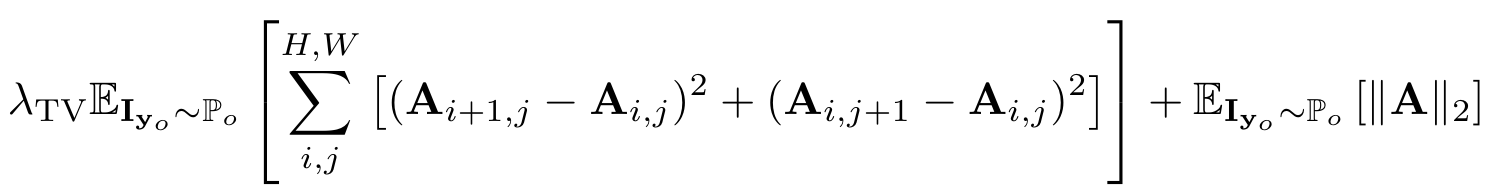
3. Conditional Expression Loss $\mathcal{L}_y$
4. Identity Loss $\mathcal{L}_{idt}$
Full Loss
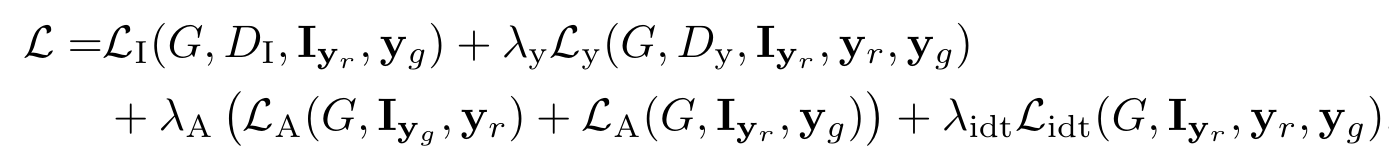
そして最終的に, 次のminimax問題を解く. $$ G^* = \arg \min_{G} \max_{D} \mathcal{L} $$
Experimental Evaluation#

References#
- GANimation
arXiv
project page