StarGAN v2 を読む | tsumli-pages

StarGAN v2: Diverse Image Synthesis for Multiple Domains
[Choi et al. CVPR 2020] という論文を読んでいきます. (本文中の図は論文より引用).

image-to-image translationのタスクにおいて, 異なるドメイン間のマッピングを学習しなければならない. そして, それらは次の要素を満たす必要がある.

生成した画像のdiversityが広い
様々にドメインに対応できる (scalability)

introduction#

既存手法では, マッピングが2つのドメイン間に限定される (scalabilityがない) という問題点があったが, StarGAN は1つのgeneratorで複数のドメインに対応するモデルを提案した. この手法では, generatorは追加のinputとしてドメインのラベルを持ち, 画像を目的のドメインに変換させる. しかし, StarGANはそれぞれのドメイン間のマッピングを学習しているだけで, データ分布のマルチモーダルな特徴を捉えているわけではない.

Method#

Framework#

ゴールは 様々な画像を生成できる1つのgenerator $G$ を訓練すること.

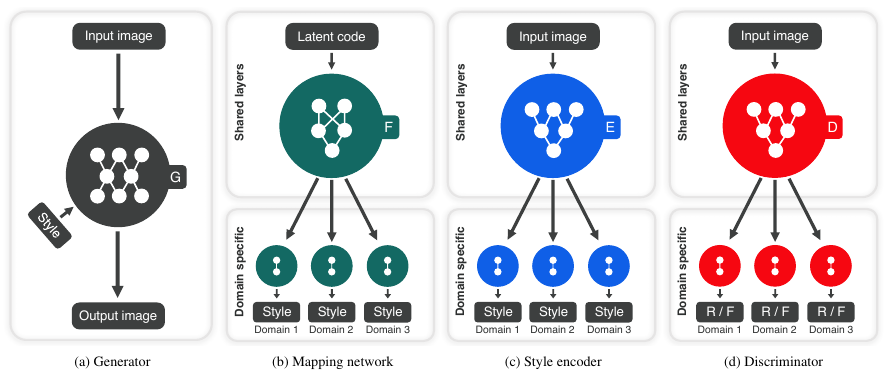
Generator (Figure 1a)

$\mathbf x \in \mathcal{X}$ を画像, $y \in \mathcal{Y}$ をドメインとする. $G$ は画像とstyle code $\mathbf s$ を引数にとり, 新たな画像を生成する (AdaINを用いて $\mathbf s$ を $G$ に与える). $y$ を $G$ に与えないことで, すべてのドメインに対応する画像が生成できる.

Mapping network (Figure 1b)

latent code $\mathbf z$ とドメイン $y$が与えられたとき, mapping network $F$ は style code $\mathbf{s}$ を生成する $$ \mathbf s = F_y (\mathbf z) $$

Style encoder (Figure 1c)

画像 $\mathbf{x}$ と対応するドメイン $y$ が与えられたとき, encoder $E$ は $\mathbf x$ に対応するstyle code $\mathbf s$ を生成する $$ \mathbf s = E_y(\mathbf x) $$

Discriminator (Figure 1d)

discriminator $D$ は複数のoutput branchを持つmulti-task discriminatorである. それぞれのbranch $D_y$ は$\mathbf x$ が $y$ に属する本当の画像か, それとも偽物の画像か判定する.

Training Objectives#

4つのロスを組み合わせたロスを用いる

1. Adversarial objective

訓練するとき, latent code $\mathbf z$ とターゲットドメイン $\tilde y \in \mathcal{Y}$ をランダムにとってくる. そして, ターゲットstyle code $\tilde{\mathbf s} = F_\tilde{y}(\mathbf{z})$ を求めたあと, $\mathbf{x}$ と $\tilde{\mathbf{s}}$ を入力として $G$ を学習させる. このとき, adversarial lossを用いる. $$ \mathcal{L}_{adv} = \mathbb{E}_{\mathbf x, y}[\log D_y(\mathbf x)] + \mathbb{E}_{\mathbf x, \tilde{y}, \mathbf{z}}[\log (1-D_\tilde{y}(G(\mathbf{x}, \tilde{\mathbf{s}})))] $$

2. Style reconstruction

生成画像からstyle codeをマッピングし, それとstyle codeの間のロスを計算する

\begin{align*} \mathcal{L}_{sty} &= \mathbb{E}_{\mathbf{x}, \tilde{y}, \mathbf{z}} [||\tilde{\mathbf{s}} - E_{\tilde{y}}(G(\mathbf{x}, \tilde{\mathbf{s}}))||_1]\\\
\end{align*}

3. Style diversification

$G$ が多様な画像を生成するためのロス \begin{align*} \mathcal{L}_{ds} &= \mathbb{E}_{\mathbf{x}, y, \mathbf{z}_1, \mathbf{z}_2} [||G(\mathbf{x}, \tilde{\mathbf{s}}_1) - G(\mathbf{x}, \tilde{\mathbf{s}}_2)||_1]\\\
\end{align*} where \begin{align*} \tilde{\mathbf{s}}_i &= F_{\tilde{y}} (\mathbf{z}_i) & \mathrm{for}\ \ i \in {1, 2}\\\
\end{align*}

4. Preserving source characteristics

$G(\mathbf{x}, \tilde{\mathbf{s}})$ が $\mathbf{x}$ におけるドメインによらない特徴 (ポーズなど) をとらえるためのロス \begin{align*} \mathcal{L}_{cyc} = \mathbb{E}_{\mathbf{x}, y, \tilde{y} \mathbf{z}} [||\mathbf{x} - G(G(\mathbf{x}, \tilde{\mathbf{s}}), \hat{\mathbf{s}})||_1] \end{align*} where \begin{align*} \hat{\mathbf{s}} &= E_y(\mathbf{x}) &\text{(入力画像}\ \mathbf{x}\ \text{に対するstyle codeの予測値)} \end{align*}

Full objective

4つのロスを組み合わせる \begin{align*} \min_{G, F, E} \max_D \ \ \mathcal{L}_{adv} + \lambda_{sty} \mathcal{L}_{sty} - \lambda_{ds} \mathcal{L}_{ds} + \lambda_{cyc} \mathcal{L}_{cyc} \end{align*}

$\lambda_\cdot$: hyper-parameter