TGAN: Synthesizing Tabular Data using Generative Adversarial Networks を読む
Synthesizing Tabular Data using Generative Adversarial Networks
[Xu et al. arXiv 2018] という論文を読んでいきます. (本文中の図は論文より引用).
tabular dataに対するGAN (TGAN) についての紹介. 様々なデータ (categorical, numericalなど) が混合したようなテーブルに対して用いることができる.
Example#
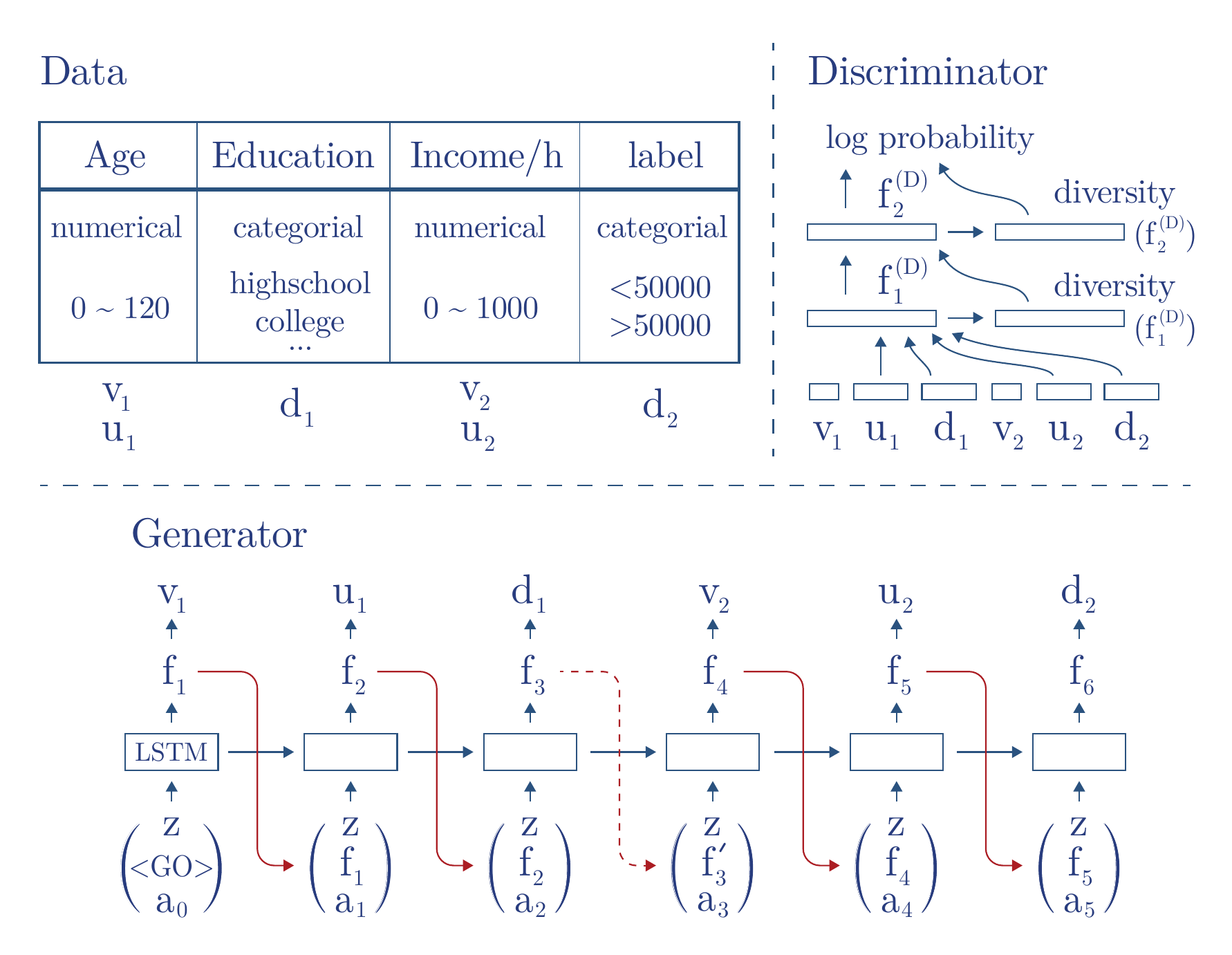
GANs for tabular data#
Synthetic table generation task#
まず, notationについて
テーブル $\mathbf{T}$ の列について $n_c$個のランダムな連続値を持つ列があるとする: $\lbrace C_1, \ldots, C_{n_c} \rbrace$.
また, $n_d$個のランダムな離散値を持つ列があるとする: $\lbrace D_1, \ldots, D_{n_d} \rbrace$.
これらの変数は未知の同時分布 $\mathbb{P} (C_{1:n_c}, D_{1: n_d})$ を持つとする.
そして, それぞれの行は次のように表される:
\begin{align}
\lbrace c_{1, j}, \ldots, c_{n_c\ ,j}\ , d_{1, j}\ , \ldots, d_{n_d\ , j} \rbrace \nonumber
\end{align}
それぞれの行は独立にサンプリングされと仮定する $\rightarrow$ シーケンシャルデータには対応していない
$$
\def\tsyn{\mathbf{T}_{synth}}
$$
次に, 目的は生成モデル $M(C_{1:n_c}\ , D_{1:n_d}\ )$ について学習することである.
そしてこの生成モデルから生成されたテーブル $\tsyn$ は次の条件を満たす必要がある.
- $\mathbf{T}$ で学習したモデルと $\tsyn$ で学習されたモデルは真のテスト用のテーブル $\mathbf{T}_{test}$ に対して同様の精度を出す
- 任意の変数間の相互情報量は $\mathbf{T}$ と $\tsyn$ で似ている
Reversible Data Transformation#
Mode-specific normalization for numerical variables
特徴量はmultimodalな分布に従っていることがあるため, 単純に特徴量を$[-1, 1]$に正規化し, tanh関数を用いて生成しようとしてもうまく行かない. そこで, Gaussian Mixture model (GMM) を用いる.
- それぞれの数値の変数 $C_i$ について $m$ 個からなる GMM を訓練する. それぞれの平均と標準偏差をそれぞれ $\eta_i^{(1)}, \ldots, \eta_i^{(m)}$, $\sigma_i^{(1)}, \ldots, \sigma_i^{(m)}$ とする.
- $m$ 個のGaussian分布を使って, $c_{i, j}$ が得られる確率分布 ($u_{i, j}^{(1)}, \ldots, u_{i, j}^{(m)}$) を計算する. ここで, $u_{i, j}$ は $m$ 個のGaussian分布に対して正規化された確率分布となる.
- $c_{i, j}$ を正規化する: $v_{i, j} = (c_{i, j} - \eta_i^{(k)}) / 2\sigma_i^{(k)}$. ここで, $k=\arg \max_k u_{i, j}^{(k)}$. そして, それぞれの値を $[-0.99, 0.99]$にクリップする.
そして, $u_i$ と $v_i$ を使って $c_i$ を表す. また, 今回の実験では $m=5$ とした.
Smoothing for categorical variables
カテゴリー特徴量にはone-hot encodingを用いる.
- 変数 $D_i$ のサンプル $d_{i, j}$ を $|D_i|$次元のone-hotベクトル $\mathbf{d}_{i, j}$ に変換する
- ノイズを加える
\begin{align} \mathbf{d}_{i, j}^{(k)} + \text{Uniform} (0, \gamma) && \text{(in this paper } \gamma = 0.2 )\nonumber \end{align} - 再び正規化する
Model and data generation#
Generator
LSTMを使う (ページ上部Fig下部参照)
- $a_t$ はattentionベースのcontextベクトルで, 前のLSTMの出力 $h_{1:t}$ の加重付き平均となっている
- 離散的な変数に対してはsoftmaxを利用し生成値とする
- 最初に使う
は特別なベクトルで, 学習可能なパラメータである
Discriminator
LeakyReLU, BatchNormを用いたFCモデルを使用
- diversity($\cdot$) はmini-batch discrimination ベクトルであり, 2層目からは前段の出力にconcatして入力ベクトルとする.
Results#
以下のデータセットについて実験を行った
- The Census-Income dataset
年収が$50kを超えるか - The KDD Cup 1999 dataset
マルウェアの侵入検知 - The Covertype dataset
森林の分類
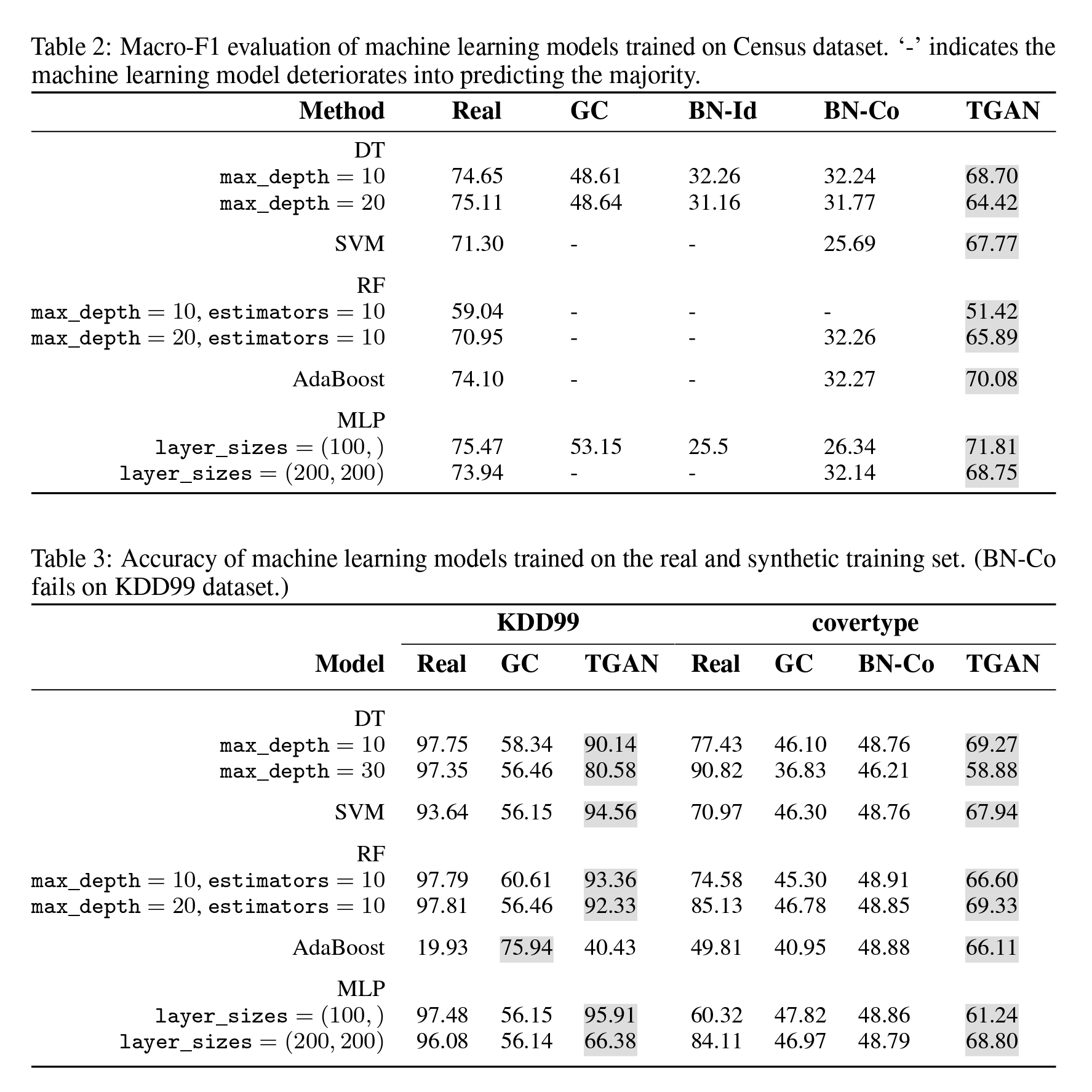
他の手法に比べてTGANで生成したデータに対して学習したモデルは, 真のデータで学習したモデルと近い評価値が得られることがわかる. $\rightarrow$ よりリアルなデータを生成できる