Lagrangian Fluid Simulation With Continuous Convolutions を読む
Lagrangian Fluid Simulation With Continuous Convolutions という論文を読んでいきます (本文中の図は論文より引用) 。 この論文では液体をグラフとして扱う…のではなくspatial convolutionを使って近傍の粒子との関係を計算します。
Continuous Convolution#
この手法では (連続的な) 畳み込み演算を点群に適用したContinuous Convolution を使用する。 $f_i$ という値を持つ位置 $x_i$ の点群 ($i = 1, \ldots, N$) について、次のように畳み込みを定義する。 $$ (f * g) (x) = \frac{1}{\psi (x)} \sum_{i \in \mathcal{N}(x, R)} a(x_i, x) f_i g (\Lambda(x_i - x)) $$
$\mathcal{N}(x, R)$ は $x$ の周りの半径 $R$ 内にある点の集合である。 また、$a$ は密度を正規化するためのスカラー関数で、次のように定義する。 $$ a(x_i, x) = \left(1 - \frac{||x_i - x||^2_2}{R^2} \right)^3 $$ $\psi(x)$ も正規化を行うためのスカラー関数で、今回は$\psi (x) = 1$ とする。
$g$ はフィルター関数で、regular gridに線形補間を掛けて連続関数にしたものである。 加えて、マッピング$\Lambda(r)$によってunit ballからunit cubeに変換する。
以下にマッピング$\Lambda(r)$の図を示す。
左側は半径$R$のspherical regionと中心に対して相対的に定義される点$r$を表している。
この点$r$をマッピング関数$\Lambda$によってregular gridに落とし込む。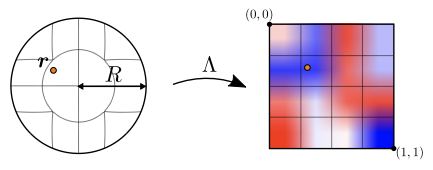
Method#
input: $(x_i^n, [1, v_i^n, \nu_i])$ ここで、$x_i^n$は$v$はベロシティ、$\nu$は粘度を表す。 Heun法をつかって中間時 (timestep=n) の位置とベロシティを計算できる。 $$ v_i^{n*} = v_i^n + \Delta t a_{\text{ext}} $$ $$ x_i^{n*} = x_i^n + \Delta t \frac{v_i^n + v_i^{n*}}{2} $$ ここで、$a_{\text{ext}}$ は加速度を表す係数である。
次に、粒子の位置、ベロシティ、粘度とオブジェクト (static particles) の情報を畳み込み層に入力することで近傍の粒子間やオブジェクトとの衝突を考えることができ、補正のための変数 $\Delta x$ を求めることができる。 最終的にtimestep=n+1のときの位置とベロシティは次のように計算 (補正) される $$ x_i^{n+1} = x_i^{n*} + \Delta x_i $$ $$ v_i^{n+1} = \frac{x_i^{n+1} - x_i^n}{\Delta t} $$
(ここらへんの流れは後で実装を見ながら確認します)
Network Architecture#
ネットワークは4層の簡単な畳み込み層で形成されている。以下にネットワークの概要を示す。 最初の層だけ特殊で、粒子の周りの特徴量をContinuous Convolution (CConv) で計算、同様にstatic particles (=obstacle) についてもCConvで計算を行う。さらに、それぞれの粒子の特徴量を線形層を使って導出する。 それぞれをconcatした後、CConv層とFC層を使って処理していき、最終的に$\Delta x$ を求める。
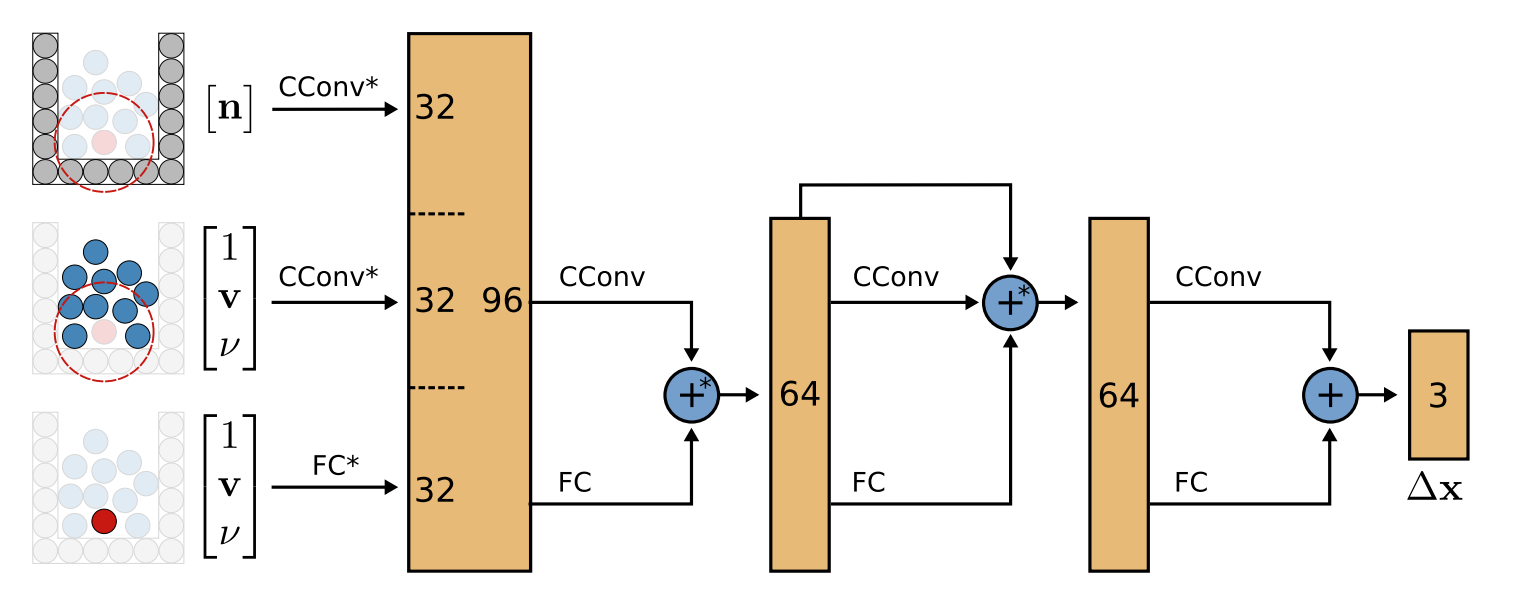
Training Procedure#
$$ \mathcal{L}^{n+1} = \sum^N_{i=1}\phi_i | x_i^{n+1} - \hat{x}_i^{n+1}|^\gamma_2 $$ ここで、$\phi_i$ はそれぞれの重みを表していて、$\phi_i = \exp(-\frac{1}{c}|\mathcal{N}(x_i^{n*})|)$ と表される (今回の実験では $c=40, \gamma=0.5$ としている) 。 このtimestep=n+1, n+2のときの損失を合わせて最終的な損失とする。 $$ \mathcal{L} = \mathcal{L}^{n+1} + \mathcal{L}^{n+2} $$
Results#

DPI-Nets との比較を示す。2つの流体がコンテナの中で衝突するというシチュエーションである。 と比べても匹敵する精度の結果が得られていることがわかる。DPI-Netsはそれぞれの粒子の運動が激しい時にあまりうまく行かない (流体がboxに衝突した時など)。 それに比べてこの手法では全体を通して安定した精度の予測が出来ている。
Implements#
github に実装が挙げられています。
MyParticleNetwork を取り上げて見てみます。このクラスの中のforward関数は次のように定義されます。 この関数では1 timestepでの処理が示されていて、位置とベロシティを計算した後にそれを補正する変数pos_correctionを推測、それらを使って最終的な位置とベロシティを導出するという流れになっています。
def forward(self, ...):
(...)
pos2, vel2 = self.integrate_pos_vel(pos, vel)
pos_correction = self.compute_correction(
pos2, vel2, feats, box, box_feats, fixed_radius_search_hash_table)
pos2_corrected, vel2_corrected = self.compute_new_pos_vel(
pos, vel, pos2, vel2, pos_correction)まず、位置とベロシティの更新 (Heun法を使用した近似) です。
def integrate_pos_vel(self, pos1, vel1):
dt = self.timestep
vel2 = vel1 + dt * self.gravity
pos2 = pos1 + dt * (vel2 + vel1) / 2
return pos2, vel2次に、compute_correctionを使って位置を推測します (若干改変を加えています) 。 ここで使われている convolution層は Continuous Convolution 、dense層はtorch.nn.Linear です。 また、2層目以降の処理にはresidual connectionが追加されていることがわかります。
def compute_correction(
self, ...
):
filter_extent = torch.tensor(self.filter_extent)
fluid_feats = [torch.ones_like(pos[:, 0:1]), vel]
(...)
self.ans_conv0_fluid = self.conv0_fluid(
fluid_feats, pos, pos, filter_extent
)
self.ans_dense0_fluid = self.dense0_fluid(
fluid_feats
)
self.ans_conv0_obstacle = self.conv0_obstacle(
box_feats, box, pos, filter_extent
)
feats = torch.cat(
[
self.ans_conv0_obstacle, self.ans_conv0_fluid, self.ans_dense0_fluid
],
axis=-1
)
self.ans_convs = [feats]
for conv, dense in zip(self.convs, self.denses):
inp_feats = F.relu(self.ans_convs[-1])
ans_conv = conv(inp_feats, pos, pos, filter_extent)
ans_dense = dense(inp_feats)
if ans_dense.shape[-1] == self.ans_convs[-1].shape[-1]:
ans = ans_conv + ans_dense + self.ans_convs[-1]
else:
ans = ans_conv + ans_dense
self.ans_convs.append(ans)
(...)
return self.ans_convs[-1]最後に、これまで計算した位置に対して補正を行い最終的な位置とベロシティを計算します。
def compute_new_pos_vel(self, pos1, vel1, pos2, vel2, pos_correction):
dt = self.timestep
pos = pos2 + pos_correction
vel = (pos - pos1) / dt
return pos, vel