Swin Transformer: Hierarchical Vision Transformer using Shifted Windows を読む
Swin Transformer: Hierarchical Vision Transformer using Shifted Windows という論文を読んでいきます (本文中の図は論文より引用) 。
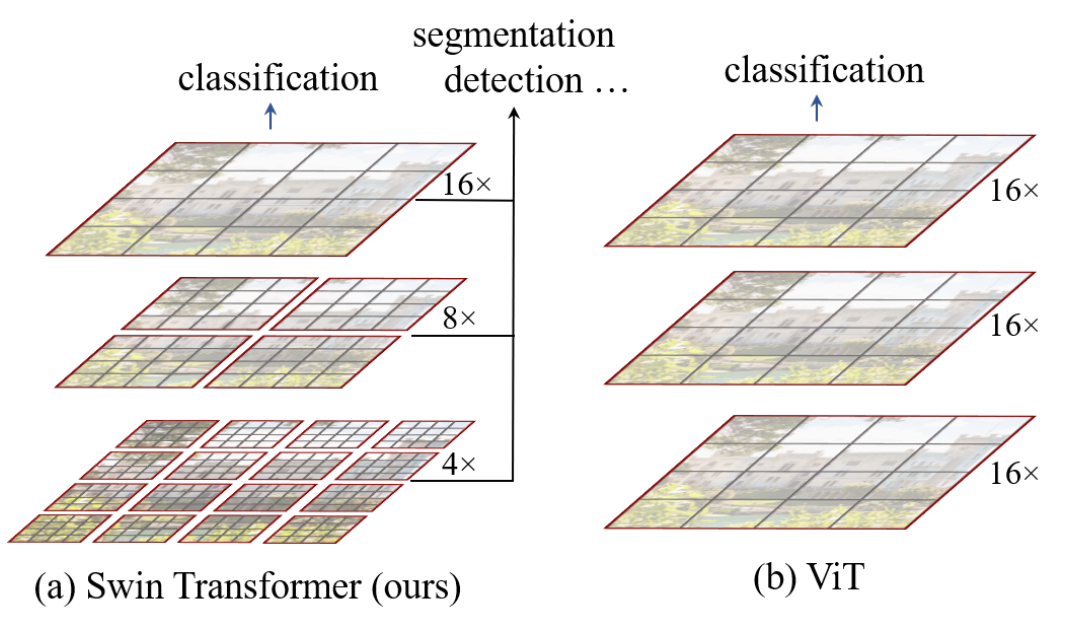
Method#
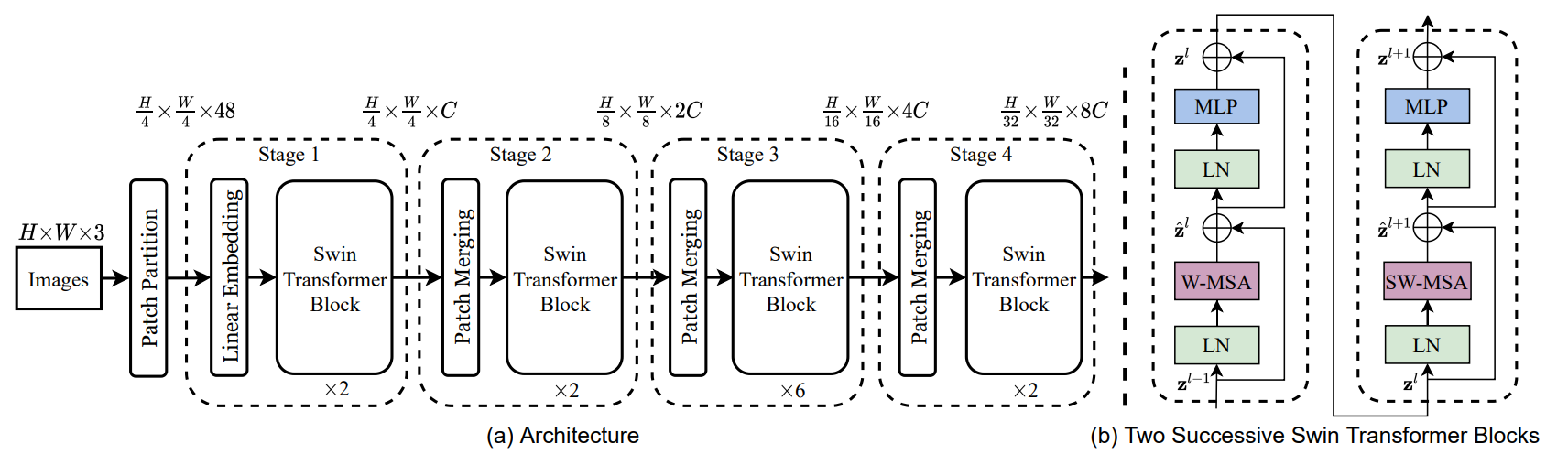
Swin Transformer Block
Multi-head self attention (MSA) をshifted-windowsのTransformerに置き換えることで作られる (図1 (b) 参照) 。
Shifted Window based Self-Attention#
Shifted window partitioning in successive blocks
window-basedなself-attentionはwindow間をまたいで情報を得ることができない。 そこで、shifted windowの分け方を提案する。
下図にshifted windowのやり方を表す。
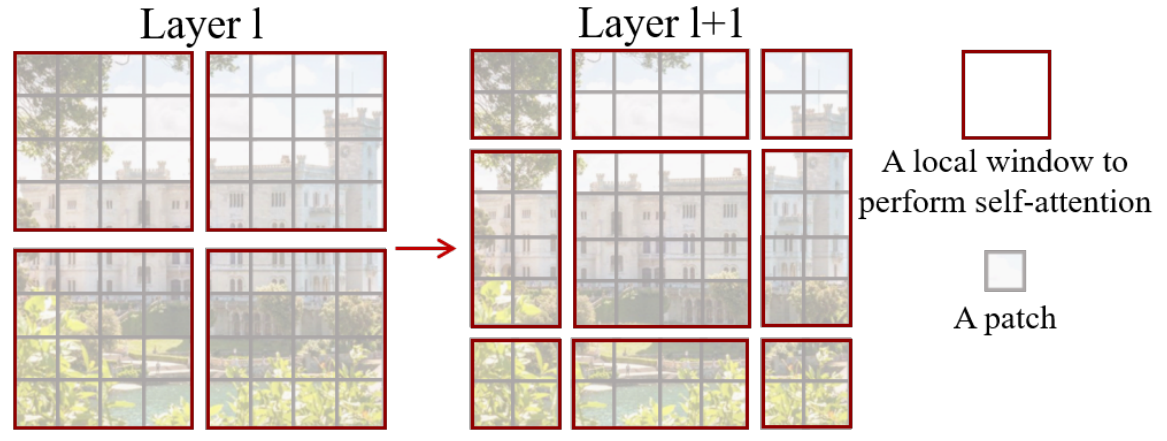
最初のモジュールは通常の分け方、つまり、左上から切り分けていく。 つまり $8 \times 8$ の特徴量を $4\times 4$ のサイズを持つwindowに切り分ける (つまり、$2\times 2$のwindowが生成される) 。その次のモジュールではwindowが $(\lfloor \frac{M}{2} \rfloor, \lfloor \frac{M}{2} \rfloor)$ だけ移動する (shifted-window)。 つまり、Swin Transformer blockでは下式のように計算される。
\begin{align*}
\hat{\mathbf{z}}^l &= \text{W-MSA} (\mathrm{LN}(\mathbf{z}^{l-1})) + \mathbf{z}^{l-1}, \\
\mathbf{z}^l &= \mathrm{MLP} (\mathrm{LN}(\hat{\mathbf{z}}^{l})) + \hat{\mathbf{z}}^{l}, \\
\hat{\mathbf{z}}^{l+1} &= \text{SW-MSA} (\mathrm{LN}(\mathbf{z}^{l})) + \mathbf{z}^{l}, \\
\mathbf{z}^{l+1} &= \mathrm{MLP} (\mathrm{LN}(\hat{\mathbf{z}}^{l+1})) + \hat{\mathbf{z}}^{l+1},
\end{align*}
Efficient batch computation for shifted configuration
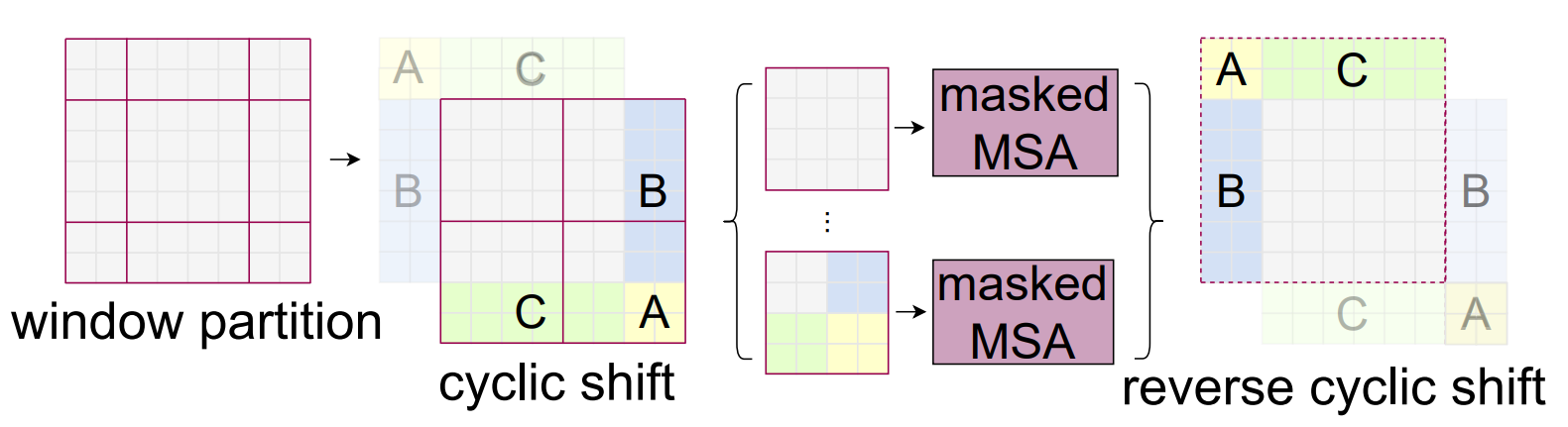
shifted windowの問題点として、windowの数が増える ($\lceil \frac{h}{M} \rceil \times\lceil \frac{w}{M} \rceil$ $\rightarrow$ $(\lceil \frac{h}{M} \rceil + 1) \times (\lceil \frac{w}{M} \rceil + 1)$) ことと、 いくつかのwindowのサイズが $M\times M$ よりも小さくなってしまうことが挙げられる。
これをナイーブな方法 (padding) ではなく解決するために、cyclic-shiftingを用いる (図3)。 このshiftを行ったあと、windowには隣接していない部分が含まれることになるが、maskingをすることでself-attentionに制限をかける。 この手法により、普通に分割したときと同じ数・サイズのwindowが生成できる。
Relative position bias
self-attentionを計算するとき、相対的なposition bias $B \in \mathbb{R}^{M^2 \times M^2}$を加える。 ここで、$M^2$ はwindowに含まれるpatchの数を表す。
つまり、次式でattentionの計算を行う \begin{align*} \text{Attention}(Q, K, V) = \text{SoftMax}(QK^\mathsf{T} / \sqrt{d} + B)V \end{align*}
相対的な位置は $[-M+1, M-1]$ の範囲に収まるため、bias matrixを $\hat{B} \in \mathbb{R}^{(2M -1) \times (2M-1)}$ をのようにパラメータ化できる。 $B$の値は $\hat{B}$ から引っ張ってくる。
Architecture Variants#
サイズと計算量のことなる複数のモデルを作ることができる。 ここで、Swin-T、Swin-Sはそれぞれ ResNet-50、ResNet-101に近いサイズである。
- Swin-T: $C=96$, layer numbers = {2, 2, 6, 2}
- Swin-S: $C=96$, layer numbers = {2, 2, 18, 2}
- Swin-B: $C=128$, layer numbers = {2, 2, 18, 2}
- Swin-L: $C=192$, layer numbers = {2, 2, 18, 2}
ここで、$C$ は最初のステージの隠れ層のチャンネルの数。
Experiment#
ImageNet-1K#
図4に、(a) 通常の方法で ImageNet-1Kで学習を行ったときと (b) ImageNet-22Kを使って事前学習を行ったときの結果を示す。
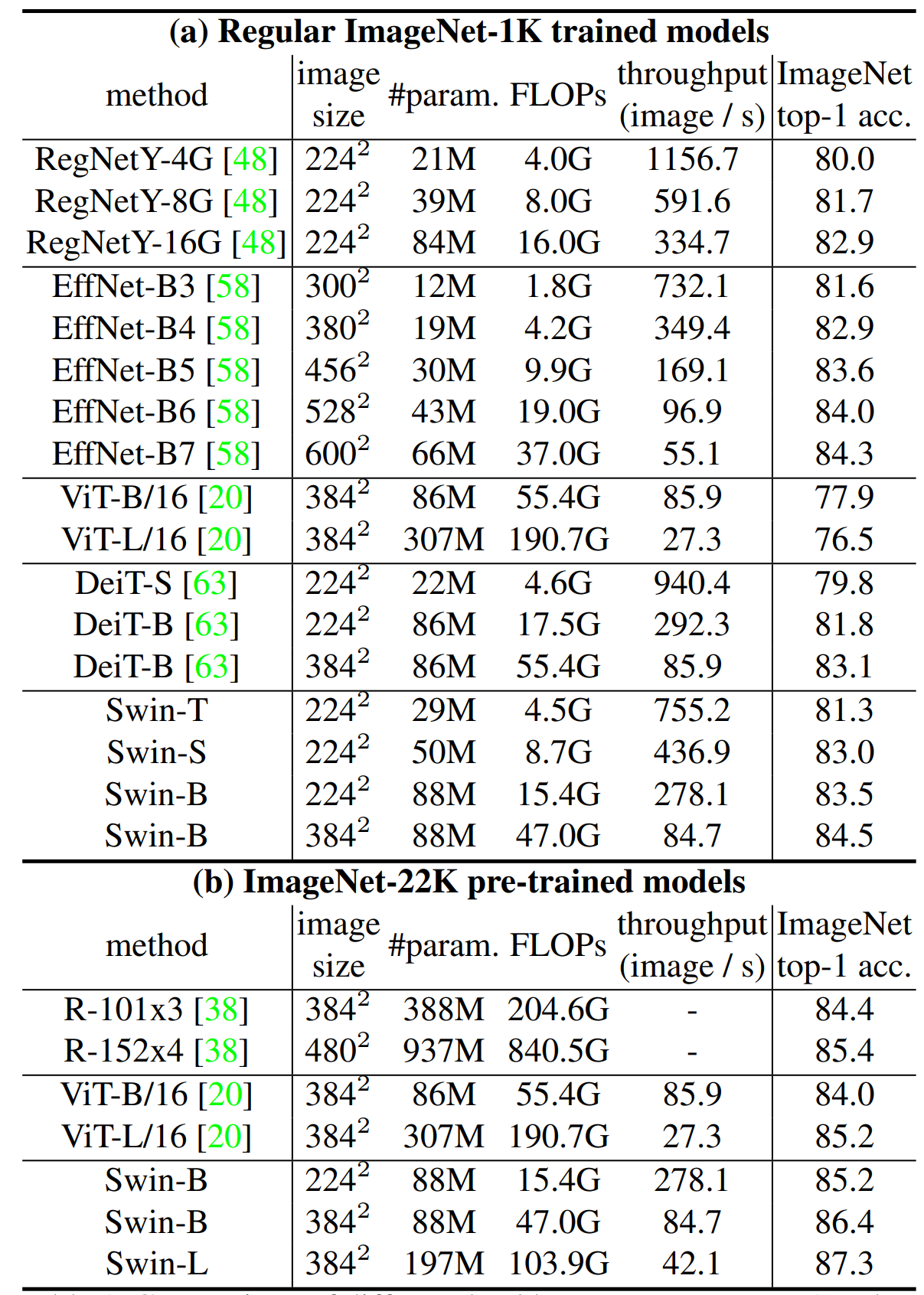
(a) について、SOTA手法である ConvNets (RegNet) や EfficientNet と比べて Swin Transformerは速度と精度のよいトレードオフ (小さくはあるが) を達成していると言える。 (b) について、事前学習を行ったとき比較手法と比べ、提案手法はとても良いトレードオフを達成している。 他にも、COCO (Object Detection) や ADE (Semantic Segmentation) についても実験を行っている (SOTAなパフォーマンスを出している)。また、それぞれのモジュールについてablation studyが行われている。
References#
Swin Transformer implementation
